RIEMANN, a program for the TI-83+ and TI-84+, approximates the area under a curve (integral) by calculating a Riemann sum, a sum of areas of simple geometric figures intersecting the curve. The program solves Riemann sums using one of four methods and displays a graph when prompted. The program itself is optimized to smaller than 1 kilobyte to reduce its memory impact. This tutorial covers the theory of Riemann sums and how to use this program.
Theory
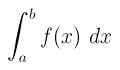
This definite integral represents the net area between a function and the x axis between x=a and x=b.
Integrals are used in the natural and social sciences, statistics, economics, finance, and more, but oftentimes they are difficult to calculate. One method of calculating integrals is to look at the basic definition of an integral, as the area underneath a curve.
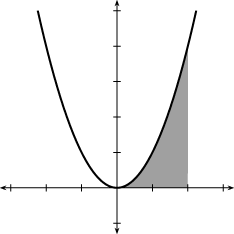
Visual representation of an integral under the curve y=x²
We can approximate this area by taking a series of rectangles and packing them underneath the curve. Unlike a smooth curve, it is easy to calculate the area of a rectangle, (base*height), and the more, smaller rectangles we use, the more accurate the approximation will be. There are actually many different ways of placing rectangles to choose from, and using trapezoids is an even more effective approach, but all of these sums converge to the actual integral. Below are 3 different visual representations of Riemann sums:
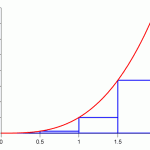
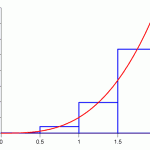
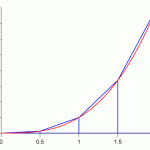
Left, Middle, and Trapezoid Riemann Sums
You can read more about Riemann sums here.
Using the RIEMANN Program
Download RIEMANN.8xp and send the file to your calculator. If you’re not familiar with this process, you can view a tutorial here. To begin, enter the equation you want to use for calculations in the Y1 variable. The Y-Variables screen can be reached by pressing . If your screen doesn’t look like this, press and make sure “Func” is selected.
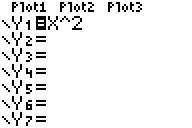
Y= Variable Screen
Press , select RIEMANN, and press to run.

Program on Home Screen
If you have your function in Y1, enter 1 to continue.
Enter 1 to draw a graph, or 2 to just solve numerically.

Enter the numbers for the left and right endpoints of the Integral.
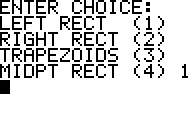
Enter the number corresponding to the method you want to use.
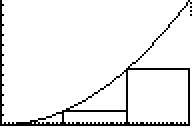
The resulting graph.
Press to continue.
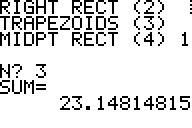
The numeric result corresponding to the area of the intervals.
You can choose to change the settings for your calculations or exit the program.
When a program is not in use, it is generally a good idea to archive it in order to conserve RAM.
PRGM:RIEMANN
ClrHome
PlotsOff
Disp "ENTER F(X) IN Y1
Disp "
Disp "CONTINUE?
Input "YES(1) NO(2) ",G
If G=2:Stop
Disp "
Disp "DRAW PICTURES?
Input "YES(1) NO(2) ",H
ClrHome
Input "LEFT ENDPOINT? ",A
Input "RIGHT ENDPOINT? ",B
If H=1:Then
A->Xmin:B->Xmax
iPart(((B-A)/20->W
If W=0:Goto Z
Lbl U
seq(X,X,A,B,W->L5
Y1(L5->L6
min(L6->Ymin
If Ymin>0:0->Ymin
max(L6->Ymax
If Ymax<0:0->Ymax
W->Xscl
iPart((abs((Ymax-Ymin)/10->Yscl
ClrList L6,L5
End
Lbl 0
ClrHome
Disp "ENTER CHOICE:
Disp "LEFT RECT (1)
Disp "RIGHT RECT (2)
Disp "TRAPEZOIDS (3)
Input "MIDPT RECT (4) ",R
Lbl 1
ClrDraw
Input "N? ",N
(B-A)/N->W
0->S:1->C
Lbl 2
If R=1:Goto 3
If R=2:Goto 4
If R=3:Goto 3
If R=4:Goto 5
Lbl 3
A+W(C-1->X
X->J:X+W->L
Goto 7
Lbl 4
A+CW->X
X-W->J:X->L
Goto 7
Lbl 5
If H≠1:Then
If N>5:Then
1->Z:W/2->H:A->X
Lbl 8
X+H->X:Y1+S->S
A+ZW->X
IS>(Z,N:Goto 8
SW->S:Goto T
End:End
A+CW-W/2->X
X-W/2->J
X+W/2->L
Goto 7
A->G:G+W->G:G->V
Lbl 9
V->X:Y1->Y:V+W->X:4Y+2Y1+S->S
V+2W->V
If V
B->X:Y1->F
(W/3)(S+E-F->S
Goto T
Lbl 7
Y1->K:K+S->S
If H=1:Goto D
Lbl I
IS>(C,N
Goto 2
If R=3:Then
A->X:Y1->P
B->X:Y1->Q
S+(Q-P)/2->S
End
W*S->S
Lbl T
Disp "SUM=",S
Pause
ClrHome
Lbl E
Menu("ENTER CHOICE","CHANGE N",1,"CHANGE METHOD",0,"QUIT",F)
Lbl F
Stop
Lbl D
If R=3:Then
Y1(L->M
Else:K->M
End
Line(J,0,J,K
Line(J,K,L,M
Line(L,M,L,0
If C=N:Pause
Goto I
Lbl Z
If B-A≤9:Then
.1->W:Else
1->W:End
Goto U

6 Responses to Riemann Sum Program for the TI-83+ and TI-84+